N1junior2025-Crypto

N1junior2025-Crypto

记录一下

Mon Sep 15 2025
2743 words · 20 minutes
CTF Crypto

这次做出了前两道，后两道主要是复现一位✌的wp（*表示赛中未出的题）

Sign (in) the ca7s

题目

因为两道题的本质都是一样的，所以我就融合成一道题一块来讲了。

点击展开代码
PYTHON
from Crypto.Util.number import bytes_to_long
from hashlib import md5
import os
FLAG1 = os.environ.get("FLAG", "flag{**redacted**}")
FLAG2 = os.environ.get("FLAG", "flag{**redacted1**}")

E = EllipticCurve(GF(0x1337_ca7_eae368ff5d702e6067aaaa77ca_ca7_1337), [0, 3])
G, n = E(1, 2), E.order()

def sign(priv, ctx, msg):
    k = bytes_to_long(ctx + md5(str(priv).encode() + msg).digest())
    z = bytes_to_long(md5(ctx + msg).digest())
    r = int((k * G).x()) % n
    s = (pow(k, -1, n) * (z + r * priv)) % n
    return r, s

def verify(pub, ctx, msg, sig):
    z = bytes_to_long(md5(ctx + msg).digest())
    r, s = sig
    if 0 < r < n and 0 < s < n:
        return r == int((pow(s, -1, n) * (z * G + r * pub)).x()) % n

def chall(level, flag):
    priv = randint(1, n - 1)
    pub = priv * G
    msg = os.urandom(64)
    

    print(f"=== level {level} ===")
    for _ in range(catalan_number(level)):
        ctx = bytes.fromhex(input('context: '))
        r, s = sign(priv, ctx, msg)
        assert verify(pub, ctx, msg, (r, s))
        if level <= 1: print('message:', msg.hex())
        if level <= 2: print('sign:', r)
        if level <= 3: print('ature:', s)
    
    r, s = map(int, input('signature: ').split())
    assert verify(pub, b'n1junior_2025', f'cat /flag{level}'.encode(), (r, s))
    print(f'flag{level}:', flag)

if __name__ == "__main__":
    chall(0, "💧")
    chall(1, "🐱")
    chall(2, FLAG1)
    chall(3, FLAG2)

解题分析

一，MD5碰撞

这里主要还是先讲这道题的主要考点——MD5哈希碰撞。

对于这道题而言，也就是：存在任意nn个不同的ctxictx_i，使得对应的哈希值是相同的；这里需要使用的工具是一个能实现“MD5碰撞”的工具（比如fastcoll）；想了解具体原理的话，可以参考Fast Collision Attack on MD5↗，我这里就直接说具体的做法（或者说——怎么通过fastcoll来生成多个符合条件的ctxictx_i）。

我是直接在win上用的fastcoll.exe，因此运行一次，最多只能生成两个符合条件的ctx。

比如说，我这里以 ”test“ 为前缀（放在test.txt里了），运行一次可以得到这样的两个ctx：

点击展开代码
PYTHON
# .\fastcoll.exe -p test.txt -o md5_msg1.txt md5_msg2.txt
ctx1 = b"test\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00)\xc0{xA\x00\x9f\xaaX\xa7\xee2\x0b\xfb\xad\x12\x9c\xb4%\xd5dVG\xa91bCQM\x90\xa6\x08\x98+\xa9\xc4^'\x1c,\x87ju\x9a\xf3\x8d+WSv\x97?\xdd-\\\xd3\x04\xbd\x1e\x80Y\xb2\x08\xe9\xeb/\xb160\xadE\x03\x7f'\xf1\xec\x01\x06\x08\x08\x9e\xff\x83\x0b%\x06.#\xc9\x1a\xf6\xbb\xecF\xfeg\xd0[\x9eX\x04\x8f\xe4Az\x1fMO\xe20\xd5&GF\x96<\xee/\xcdfVb\x0e$\xba8\x9cg"
ctx2 = b"test\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00)\xc0{xA\x00\x9f\xaaX\xa7\xee2\x0b\xfb\xad\x12\x9c\xb4%UdVG\xa91bCQM\x90\xa6\x08\x98+\xa9\xc4^'\x1c,\x87ju\x9a\xf3\r,WSv\x97?\xdd-\\\xd3\x04\xbd\x1e\x00Y\xb2\x08\xe9\xeb/\xb160\xadE\x03\x7f'\xf1\xec\x01\x06\x08\x08\x9e\xff\x83\x8b%\x06.#\xc9\x1a\xf6\xbb\xecF\xfeg\xd0[\x9eX\x04\x8f\xe4Az\x1fMO\xe2\xb0\xd4&GF\x96<\xee/\xcdfVb\x0e\xa4\xba8\x9cg"

我们去查看后缀（除去前缀外的部分）会发现——长度一致但内容不同；而且这两个ctx长度都是64bytes的整数倍（刚好是一个哈希分组块的长度）

PYTHON
# len("test") = 4
print(len(ctx1[4:])==len(ctx2[4:]), ctx1[4:]==ctx2[4:])
# True False

而这就是我们通过fastcoll做这道题的一个关键点了。

假如我们此时以ctx1为我们的前缀，再次使用fastcoll去生成ctx3和ctx4，并检查此时的后缀（与ctx1相比多出的部分）会发现——仍然是长度一致但内容不同；而且这两个ctx长度依然都是64bytes的整数倍。

点击展开代码
PYTHON
# .\fastcoll.exe -p test.txt -o md5_msg1.txt md5_msg2.txt
ctx3 = b"test\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00)\xc0{xA\x00\x9f\xaaX\xa7\xee2\x0b\xfb\xad\x12\x9c\xb4%\xd5dVG\xa91bCQM\x90\xa6\x08\x98+\xa9\xc4^'\x1c,\x87ju\x9a\xf3\x8d+WSv\x97?\xdd-\\\xd3\x04\xbd\x1e\x80Y\xb2\x08\xe9\xeb/\xb160\xadE\x03\x7f'\xf1\xec\x01\x06\x08\x08\x9e\xff\x83\x0b%\x06.#\xc9\x1a\xf6\xbb\xecF\xfeg\xd0[\x9eX\x04\x8f\xe4Az\x1fMO\xe20\xd5&GF\x96<\xee/\xcdfVb\x0e$\xba8\x9cg\xbe\x98\xa9\xfcW\x1c=\xb6\xbbE\xc0\xdf\xd5\xf7\x82\xea\xc85\xeb\x96\xdb\xc6\xaa\x9a!\xf69a\x15(\x1b'\xc6\xf9\xb5\xb8^\xcd?x\x8b\xe4O\x12\xee\x11!G\x8a\xcf*\xdc={\x0f;\xc9\xef\x9ba\xaf5\xd9B\xfa\xafx\xaf\xd4\x83\xc5\xb9\xc3\r\xbf\x03\xf7\xcfj8G\x11cWpY\x93(+\xb3\x10w\x06`\xa8\xc6\xcbKN\x14\xaf\xc7[^:\t\x0c\\\x8b_\x17\xe2\xa8\x81\x0c\xb3$\x86]IblU\xd4\x86\x04\x15\xcc"
ctx4 = b"test\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00)\xc0{xA\x00\x9f\xaaX\xa7\xee2\x0b\xfb\xad\x12\x9c\xb4%\xd5dVG\xa91bCQM\x90\xa6\x08\x98+\xa9\xc4^'\x1c,\x87ju\x9a\xf3\x8d+WSv\x97?\xdd-\\\xd3\x04\xbd\x1e\x80Y\xb2\x08\xe9\xeb/\xb160\xadE\x03\x7f'\xf1\xec\x01\x06\x08\x08\x9e\xff\x83\x0b%\x06.#\xc9\x1a\xf6\xbb\xecF\xfeg\xd0[\x9eX\x04\x8f\xe4Az\x1fMO\xe20\xd5&GF\x96<\xee/\xcdfVb\x0e$\xba8\x9cg\xbe\x98\xa9\xfcW\x1c=\xb6\xbbE\xc0\xdf\xd5\xf7\x82\xea\xc85\xeb\x16\xdb\xc6\xaa\x9a!\xf69a\x15(\x1b'\xc6\xf9\xb5\xb8^\xcd?x\x8b\xe4O\x12\xee\x91!G\x8a\xcf*\xdc={\x0f;\xc9\xef\x9b\xe1\xaf5\xd9B\xfa\xafx\xaf\xd4\x83\xc5\xb9\xc3\r\xbf\x03\xf7\xcfj8G\x11c\xd7pY\x93(+\xb3\x10w\x06`\xa8\xc6\xcbKN\x14\xaf\xc7[^:\t\x0c\\\x8b\xdf\x16\xe2\xa8\x81\x0c\xb3$\x86]IblUT\x86\x04\x15\xcc"

print(len(t3[len(t1):])==len(t4[len(t1):]), t1[len(t1):]==t2[len(t1):])
# True True

# 这里假设以"test"为前缀来看
print(len(t3[4:])==len(t4[4:]), t1[4:]==t2[4:])
# True False

看到这的师傅，应该会有这么个猜想：因为此时是以ctx1为前缀生成的ctx3和ctx4，且ctx3和ctx4的后缀也跟前面ctx1和ctx2的后缀是同一规律；那会不会ctx3和ctx4的后缀给ctx2也能生成同样的MD5值呢？

答案是肯定的：

点击展开代码
PYTHON
from hashlib import md5
ctx1 = b"test\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00)\xc0{xA\x00\x9f\xaaX\xa7\xee2\x0b\xfb\xad\x12\x9c\xb4%\xd5dVG\xa91bCQM\x90\xa6\x08\x98+\xa9\xc4^'\x1c,\x87ju\x9a\xf3\x8d+WSv\x97?\xdd-\\\xd3\x04\xbd\x1e\x80Y\xb2\x08\xe9\xeb/\xb160\xadE\x03\x7f'\xf1\xec\x01\x06\x08\x08\x9e\xff\x83\x0b%\x06.#\xc9\x1a\xf6\xbb\xecF\xfeg\xd0[\x9eX\x04\x8f\xe4Az\x1fMO\xe20\xd5&GF\x96<\xee/\xcdfVb\x0e$\xba8\x9cg"
ctx2 = b"test\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00)\xc0{xA\x00\x9f\xaaX\xa7\xee2\x0b\xfb\xad\x12\x9c\xb4%UdVG\xa91bCQM\x90\xa6\x08\x98+\xa9\xc4^'\x1c,\x87ju\x9a\xf3\r,WSv\x97?\xdd-\\\xd3\x04\xbd\x1e\x00Y\xb2\x08\xe9\xeb/\xb160\xadE\x03\x7f'\xf1\xec\x01\x06\x08\x08\x9e\xff\x83\x8b%\x06.#\xc9\x1a\xf6\xbb\xecF\xfeg\xd0[\x9eX\x04\x8f\xe4Az\x1fMO\xe2\xb0\xd4&GF\x96<\xee/\xcdfVb\x0e\xa4\xba8\x9cg"
ctx3 = b"test\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00)\xc0{xA\x00\x9f\xaaX\xa7\xee2\x0b\xfb\xad\x12\x9c\xb4%\xd5dVG\xa91bCQM\x90\xa6\x08\x98+\xa9\xc4^'\x1c,\x87ju\x9a\xf3\x8d+WSv\x97?\xdd-\\\xd3\x04\xbd\x1e\x80Y\xb2\x08\xe9\xeb/\xb160\xadE\x03\x7f'\xf1\xec\x01\x06\x08\x08\x9e\xff\x83\x0b%\x06.#\xc9\x1a\xf6\xbb\xecF\xfeg\xd0[\x9eX\x04\x8f\xe4Az\x1fMO\xe20\xd5&GF\x96<\xee/\xcdfVb\x0e$\xba8\x9cg\xbe\x98\xa9\xfcW\x1c=\xb6\xbbE\xc0\xdf\xd5\xf7\x82\xea\xc85\xeb\x96\xdb\xc6\xaa\x9a!\xf69a\x15(\x1b'\xc6\xf9\xb5\xb8^\xcd?x\x8b\xe4O\x12\xee\x11!G\x8a\xcf*\xdc={\x0f;\xc9\xef\x9ba\xaf5\xd9B\xfa\xafx\xaf\xd4\x83\xc5\xb9\xc3\r\xbf\x03\xf7\xcfj8G\x11cWpY\x93(+\xb3\x10w\x06`\xa8\xc6\xcbKN\x14\xaf\xc7[^:\t\x0c\\\x8b_\x17\xe2\xa8\x81\x0c\xb3$\x86]IblU\xd4\x86\x04\x15\xcc"
ctx4 = b"test\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00)\xc0{xA\x00\x9f\xaaX\xa7\xee2\x0b\xfb\xad\x12\x9c\xb4%\xd5dVG\xa91bCQM\x90\xa6\x08\x98+\xa9\xc4^'\x1c,\x87ju\x9a\xf3\x8d+WSv\x97?\xdd-\\\xd3\x04\xbd\x1e\x80Y\xb2\x08\xe9\xeb/\xb160\xadE\x03\x7f'\xf1\xec\x01\x06\x08\x08\x9e\xff\x83\x0b%\x06.#\xc9\x1a\xf6\xbb\xecF\xfeg\xd0[\x9eX\x04\x8f\xe4Az\x1fMO\xe20\xd5&GF\x96<\xee/\xcdfVb\x0e$\xba8\x9cg\xbe\x98\xa9\xfcW\x1c=\xb6\xbbE\xc0\xdf\xd5\xf7\x82\xea\xc85\xeb\x16\xdb\xc6\xaa\x9a!\xf69a\x15(\x1b'\xc6\xf9\xb5\xb8^\xcd?x\x8b\xe4O\x12\xee\x91!G\x8a\xcf*\xdc={\x0f;\xc9\xef\x9b\xe1\xaf5\xd9B\xfa\xafx\xaf\xd4\x83\xc5\xb9\xc3\r\xbf\x03\xf7\xcfj8G\x11c\xd7pY\x93(+\xb3\x10w\x06`\xa8\xc6\xcbKN\x14\xaf\xc7[^:\t\x0c\\\x8b\xdf\x16\xe2\xa8\x81\x0c\xb3$\x86]IblUT\x86\x04\x15\xcc"

print(md5(ctx3).hexdigest())
print(md5(ctx2+ctx3[len(ctx2):]).hexdigest())
print(md5(ctx2+ctx4[len(ctx2):]).hexdigest())
"""
f5624faf5b3f1d67342a20d7bbeb0f81
f5624faf5b3f1d67342a20d7bbeb0f81
f5624faf5b3f1d67342a20d7bbeb0f81
"""

此时我们便获得了22=42^2=4个可能的ctxictx_i，那假如以ctx3为前缀继续呢？

那便如下图所示：

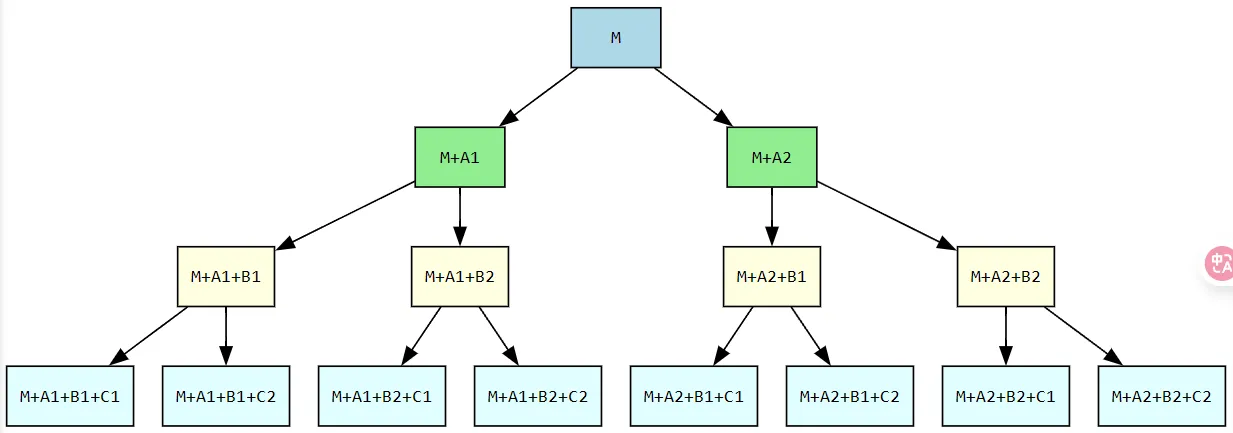
image-20250915160047906

此时就有23=82^3=8个可能的ctxictx_i

组合方式为：

ctxi=M+(A1/A2)+(B1/B2)+(C1/C2)+(D1/D2)ctx_i=M+(A_1/A_2)+(B_1/B_2)+(C_1/C_2)+(D_1/D_2)

于是就说明：每次生成的两个后缀和前一次的未用前缀拼起来，可以的得到此时的同一md5值的两个串。

所以我们手动nn次fastcoll，就可以组合出2n2^n个我们需要的ctxictx_i（当然，其实maple师傅之前有出过一道题，对应的解题脚本↗里就实现了这一功能）。

二，具体题目

题目中提供数据的部分是这里：

PYTHON
# 这里依据当时做题的时候测出来的情况而写的
def catalan_number(L):
    if L in [0, 1]:
        return 1
    elif L == 2:
        return 2
    else:
        return 5

def sign(priv, ctx, msg):
    k = bytes_to_long(ctx + md5(str(priv).encode() + msg).digest())
    z = bytes_to_long(md5(ctx + msg).digest())
    r = int((k * G).x()) % n
    s = (pow(k, -1, n) * (z + r * priv)) % n
    return r, s

def verify(pub, ctx, msg, sig):
    z = bytes_to_long(md5(ctx + msg).digest())
    r, s = sig
    if 0 < r < n and 0 < s < n:
        return r == int((pow(s, -1, n) * (z * G + r * pub)).x()) % n

def chall(level, flag):
    priv = randint(1, n - 1)
    pub = priv * G
    msg = os.urandom(64)
    
    print(f"=== level {level} ===")
    for _ in range(catalan_number(level)):
        ctx = bytes.fromhex(input('context: '))
        r, s = sign(priv, ctx, msg)
        assert verify(pub, ctx, msg, (r, s))
        if level <= 1: print('message:', msg.hex())
        if level <= 2: print('sign:', r)
        if level <= 3: print('ature:', s)
    
    r, s = map(int, input('signature: ').split())
    assert verify(pub, b'n1junior_2025', f'cat /flag{level}'.encode(), (r, s))
    print(f'flag{level}:', flag)

这题的签名算法是ECDSA，题目是让我们根据一定的交互次数与交互后的数据来算出私钥priv，从而伪造签名通过verify的验证。

因此我就按给的level来逐一说明。

Level 0/1

此时题目只给了我们一次输入ctx的机会，并获得一组msg、sign、ature（后两个是r和s）。

而我们知道ECDSA的签名是这样的：

H=md5(ctx+msg), k=ctx+md5(priv+msg) mod ns=k−1(H+r∗d) mod nH=md5(ctx + msg),\ k=ctx+md5(priv+msg)\ mod\ n\\ s=k^{-1}(H+r*d)\ mod\ n

于是我们就可以得到：

d=(s∗k−H)∗r−1 mod nd=(s*k-H)*r^{-1}\ mod\ n

不过这里会有个问题：因为r = int((k * G).x()) % n，假如使用E.lift_x(r)，我们只是得到一个坐标 (x, y)(x,\ y)，但有可能我们需要的正确坐标是 (x, −y)(x,\ -y)。

好在这里条件充分，且有k = bytes_to_long(ctx + md5(str(priv).encode() + msg).digest())，所以我们可以验证这个式子是否成立来判断取 (x, y)(x,\ y)还是 (x, −y)(x,\ -y)，最后就是去仿造r和s了。

PYTHON
# sage 10.6

# =============Level 0=============
io.recvuntil(b"context: ")
io.sendline(b"")
msg = bytes.fromhex(io.recvline().split()[-1].decode())
r = eval(io.recvline().split()[-1].decode())
s = eval(io.recvline().split()[-1].decode())

# s = (pow(k, -1, n) * (z + r * priv)) % n
z = bytes_to_long(md5(msg).digest())
k1 = (E.lift_x(Integer(r))).log(G)
k2 = (-E.lift_x(Integer(r))).log(G)
priv = ((s*k1-z)*invert(r, n))%n
priv_i = ((s*k1-z)*invert(r, n))%n
if k1 != bytes_to_long(md5(str(priv).encode() + msg).digest()):
    priv = priv_i
r, s = Sign(priv, b'n1junior_2025', f'cat /flag{level}'.encode())
io.recvuntil(b"signature: ")
io.sendline(b" ".join([str(r).encode(), str(s).encode()]))
c1 = io.recvline().decode()
print(c1)
level += 1
# flag0: 💧

# =============Level 1=============
io.recvuntil(b"context: ")
io.sendline(b"")
msg = bytes.fromhex(io.recvline().split()[-1].decode())
r = eval(io.recvline().split()[-1].decode())
s = eval(io.recvline().split()[-1].decode())

# s = (pow(k, -1, n) * (z + r * priv)) % n
z = bytes_to_long(md5(msg).digest())
k1 = (E.lift_x(Integer(r))).log(G)
k2 = (-E.lift_x(Integer(r))).log(G)
priv = ((s*k1-z)*invert(r, n))%n
priv_i = ((s*k1-z)*invert(r, n))%n
if k1 != bytes_to_long(md5(str(priv).encode() + msg).digest()):
    priv = priv_i
r, s = Sign(priv, b'n1junior_2025', f'cat /flag{level}'.encode())
io.recvuntil(b"signature: ")
io.sendline(b" ".join([str(r).encode(), str(s).encode()]))
c1 = io.recvline().decode()
print(c1)
level += 1
# flag1: 🐱

Level 2

此时题目给了我们两次输入ctx的机会，并获得两组sign、ature（也就是r和s）。

而前面介绍MD5碰撞的时候有说到可以利用n次fastcoll来构造2n2^n个我们需要的ctxictx_i。

于是我们就可以构造出两个ctx，直接传到靶机上去获取数据（毕竟ctx都是64bytes的整数倍，所以不影响最后的哈希值的一致），从而就有下列推导：

s1∗k1=(H+r1∗d) mod ns2∗k2=(H+r2∗d) mod ns2∗k2−s1∗k1=[(r2−r1)∗d] mod nd=(s2∗k2−s1∗k1)∗(r2−r1)−1 mod n\begin{align*} s_1*k_1&=(H+r_1*d)\ mod\ n\\ s_2*k_2&=(H+r_2*d)\ mod\ n\\ s_2*k_2-s_1*k_1&=[(r_2-r_1)*d]\ mod\ n\\ d&=(s_2*k_2-s_1*k_1)*(r_2-r_1)^{-1}\ mod\ n \end{align*}

这里同样会有坐标 (x, y)(x,\ y)与坐标 (x, −y)(x,\ -y)的取舍。

不过，我们如果去写代码去测试正确的kk与我们计算的kk的区别，会发现这样一个结论：ctx1∗25616 mod nctx_1*256^{16}\ mod\ n与正确的kk的绝对值一定是最小的！

所以我们可以由此来判断取 (x, y)(x,\ y)还是 (x, −y)(x,\ -y)，最后就是去仿造r和s了。

PYTHON
# sage 10.6

# =============Level 2=============
t1 = 
t2 = 
tt1 = int(bytes_to_long(t1)*256**16%n)
tt2 = int(bytes_to_long(t2)*256**16%n)
io.recvuntil(b"context: ")
io.sendline(t1.hex().encode())
r1 = eval(io.recvline().split()[-1].decode())
s1 = eval(io.recvline().split()[-1].decode())

io.recvuntil(b"context: ")
io.sendline(t2.hex().encode())
r2 = eval(io.recvline().split()[-1].decode())
s2 = eval(io.recvline().split()[-1].decode())

# s = (pow(k, -1, n) * (z + r * priv)) % n
k1 = (E.lift_x(Integer(r1))).log(G)
k2 = (E.lift_x(Integer(r2))).log(G)
k11 = (-E.lift_x(Integer(r1))).log(G)
k22 = (-E.lift_x(Integer(r2))).log(G)
if abs(tt1-k1) > abs(tt1-k11):
    k1 = k11
if abs(tt2-k2) > abs(tt2-k22):
    k2 = k22
priv = ((s1*k1-s2*k2)*invert(r1-r2, n))%n
r, s = Sign(priv, b'n1junior_2025', f'cat /flag{level}'.encode())
io.recvuntil(b"signature: ")
io.sendline(b" ".join([str(r).encode(), str(s).encode()]))
c2 = io.recvline().decode()
print(c2)
level += 1
# flag2: flag{**redacted**}

Level 3

此时题目给了我们五次输入ctx的机会，并获得五个ature（即s）。

与Level2一样，构造五个ctxctx，直接传到靶机上去获取数据，来得到五个ature（即s）。

此时我们便有这五个式子（我假设叫方程组1）：

s1∗k1=(H+r1∗d) mod ns2∗k2=(H+r2∗d) mod ns3∗k3=(H+r3∗d) mod ns4∗k4=(H+r4∗d) mod ns5∗k5=(H+r5∗d) mod n\begin{align*} s_1*k_1&=(H+r_1*d)\ mod\ n\\ s_2*k_2&=(H+r_2*d)\ mod\ n\\ s_3*k_3&=(H+r_3*d)\ mod\ n\\ s_4*k_4&=(H+r_4*d)\ mod\ n\\ s_5*k_5&=(H+r_5*d)\ mod\ n \end{align*}

此时，未知数的数量是大于方程数量的（12>5）。但是，我们别忘了这个：

k1=ctx1∗25616+md5(priv+msg)k2=ctx2∗25616+md5(priv+msg)k3=ctx3∗25616+md5(priv+msg)k4=ctx4∗25616+md5(priv+msg)k5=ctx5∗25616+md5(priv+msg)\begin{align*} k_1&={ctx}_1*256^{16} + md5(priv+msg)\\ k_2&={ctx}_2*256^{16} + md5(priv+msg)\\ k_3&={ctx}_3*256^{16} + md5(priv+msg)\\ k_4&={ctx}_4*256^{16} + md5(priv+msg)\\ k_5&={ctx}_5*256^{16} + md5(priv+msg) \end{align*}

如果我们以k0k_0为我们的未知量，那么我们便有（我假设叫方程组2）：

k1=k0k2=k0+(ctx2−ctx1)∗25616k3=k0+(ctx3−ctx1)∗25616k4=k0+(ctx4−ctx1)∗25616k5=k0+(ctx5−ctx1)∗25616\begin{align*} k_1&=k_0\\ k_2&=k_0+({ctx}_2-{ctx}_1)*256^{16}\\ k_3&=k_0+({ctx}_3-{ctx}_1)*256^{16}\\ k_4&=k_0+({ctx}_4-{ctx}_1)*256^{16}\\ k_5&=k_0+({ctx}_5-{ctx}_1)*256^{16} \end{align*}

此时未知数的数量就减少为8个，仍大于我们的方程数。

于是还需要结合这个：

r1=(k1G)xr2=(k2G)xr3=(k3G)xr4=(k4G)xr5=(k5G)x\begin{align*} r_1&=(k_1G)_x\\ r_2&=(k_2G)_x\\ r_3&=(k_3G)_x\\ r_4&=(k_4G)_x\\ r_5&=(k_5G)_x \end{align*}

此时便有：

r1=(k0G)xr2=[k0G+(ctx2−ctx1)G]x=[k0G+A]xr3=[k0G+(ctx3−ctx1)G]x=[k0G+B]xr4=[k0G+(ctx4−ctx1)G]x=[k0G+C]xr5=[k0G+(ctx5−ctx1)G]x=[k0G+D]x\begin{align*} r_1&=(k_0G)_x\\ r_2&=[k_0G+({ctx}_2-{ctx}_1)G]_x=[k_0G+A]_x\\ r_3&=[k_0G+({ctx}_3-{ctx}_1)G]_x=[k_0G+B]_x\\ r_4&=[k_0G+({ctx}_4-{ctx}_1)G]_x=[k_0G+C]_x\\ r_5&=[k_0G+({ctx}_5-{ctx}_1)G]_x=[k_0G+D]_x \end{align*}

此时的未知数数量就减少到3个，小于我们的方程数。

但是，这样实现起来，还需要自己实现一个椭圆运算（因为k0k_0可不是数值），显得过于复杂了，那有没有更简单的方法呢？有的，兄弟有的！

既然是椭圆运算了，那不妨设x0x_0和y0y_0使得：

(k0G)=(x0, y0)(k_0G)=(x_0,\ y_0)

于是便有（我假设叫方程组3）：

r1=x0r2=[(Ay−y0Ax−x0)2−(x0+Ax)] mod nr3=[(By−y0Bx−x0)2−(x0+Bx)] mod nr4=[(Cy−y0Cx−x0)2−(x0+Cx)] mod nr5=[(Dy−y0Dx−x0)2−(x0+Dx)] mod n\begin{align*} r_1&=x_0\\ r_2&=[(\frac{A_y-y_0}{A_x-x_0})^2-(x_0+A_x)]\ mod\ n\\ r_3&=[(\frac{B_y-y_0}{B_x-x_0})^2-(x_0+B_x)]\ mod\ n\\ r_4&=[(\frac{C_y-y_0}{C_x-x_0})^2-(x_0+C_x)]\ mod\ n\\ r_5&=[(\frac{D_y-y_0}{D_x-x_0})^2-(x_0+D_x)]\ mod\ n \end{align*}

结合方程组1、方程组2、方程组3，整理一下就有：

f1=s1∗k1−H−x0∗df2=s2∗k2∗(Ax−x0)2−H∗(Ax−x0)2−[(Ay−y0)2−(x0+Ax)∗(Ax−x0)2]∗df3=s3∗k3∗(Bx−x0)2−H∗(Bx−x0)2−[(By−y0)2−(x0+Bx)∗(Bx−x0)2]∗df4=s4∗k4∗(Cx−x0)2−H∗(Cx−x0)2−[(Cy−y0)2−(x0+Cx)∗(Cx−x0)2]∗df5=s5∗k5∗(Dx−x0)2−H∗(Dx−x0)2−[(Dy−y0)2−(x0+Dx)∗(Dx−x0)2]∗d\begin{align*} f_1&=s_1*k_1-H-x_0*d\\ f_2&=s_2*k_2*(A_x-x_0)^2-H*(A_x-x_0)^2-[(A_y-y_0)^2-(x_0+A_x)*(A_x-x_0)^2]*d\\ f_3&=s_3*k_3*(B_x-x_0)^2-H*(B_x-x_0)^2-[(B_y-y_0)^2-(x_0+B_x)*(B_x-x_0)^2]*d\\ f_4&=s_4*k_4*(C_x-x_0)^2-H*(C_x-x_0)^2-[(C_y-y_0)^2-(x_0+C_x)*(C_x-x_0)^2]*d\\ f_5&=s_5*k_5*(D_x-x_0)^2-H*(D_x-x_0)^2-[(D_y-y_0)^2-(x_0+D_x)*(D_x-x_0)^2]*d \end{align*}

此时的未知数数量为5个，刚好就是我们的方程数。

然后我们再用下groebner_basis，计算出dd然后去伪造r跟s就行了。

PYTHON
# sage 10.6

# =============Level 3=============
tt = []
t_int = [bytes_to_long(i) for i in tt]
io.recvuntil(b"context: ")
sh = []
R = PolynomialRing(GF(n), "k0, z, x0, y0, d")
k0, z, x0, y0, d = R.gens()
io.sendline(tt[0].hex().encode())
sh.append(eval(io.recvline().split()[-1].decode()))
eqs = [y0**2-(x0**3+3), sh[0]*k0-(z+x0*d)]
for i in range(1, 5):
    io.recvuntil(b"context: ")
    ki = k0 + (t_int[i]-t_int[0])*(256**16)
    del_k = (t_int[i]-t_int[0])*(256**16)*G
    del_kx, del_ky = del_k.xy()
    sl = (del_ky-y0)/(del_kx-x0)
    xi = sl**2-x0-del_kx
    io.sendline(tt[i].hex().encode())
    sh.append(eval(io.recvline().split()[-1].decode()))
    eqs.append((sh[i]*ki-(z+xi*d)).numerator())
# print("over")
I = R.ideal(eqs)
priv = I.groebner_basis()[-1]
# print(priv)
priv = int(-priv.coefficients()[-1])
r, s = Sign(priv, b'n1junior_2025', f'cat /flag{level}'.encode())
io.recvuntil(b"signature: ")
io.sendline(b" ".join([str(r).encode(), str(s).encode()]))
c3 = io.recvline().decode()
print(c3)
# flag3: flag{**redacted1**}

exp

点击展开代码
PYTHON
# sage10.6
from pwn import *
from sage.all import *
from gmpy2 import invert
from Crypto.Util.number import *
from hashlib import md5


def Sign(priv, ctx, msg):
    k = bytes_to_long(ctx + md5(str(priv).encode() + msg).digest())
    z = bytes_to_long(md5(ctx + msg).digest())
    r = int((k * G).x()) % n
    s = (pow(k, -1, n) * (z + r * priv)) % n
    return r, s


E = EllipticCurve(GF(0x1337_ca7_eae368ff5d702e6067aaaa77ca_ca7_1337), [0, 3])
G, n = E(1, 2), E.order()
# io = remote("60.205.163.215", int(27074))
io = process(['sage', 'test.sage'])
level = 0


# =============Level 0=============
io.recvuntil(b"context: ")
io.sendline(b"")
msg = bytes.fromhex(io.recvline().split()[-1].decode())
r = eval(io.recvline().split()[-1].decode())
s = eval(io.recvline().split()[-1].decode())

# s = (pow(k, -1, n) * (z + r * priv)) % n
z = bytes_to_long(md5(msg).digest())
k1 = (E.lift_x(Integer(r))).log(G)
k2 = (-E.lift_x(Integer(r))).log(G)
priv = ((s*k1-z)*invert(r, n))%n
priv_i = ((s*k1-z)*invert(r, n))%n
if k1 != bytes_to_long(md5(str(priv).encode() + msg).digest()):
    priv = priv_i
r, s = Sign(priv, b'n1junior_2025', f'cat /flag{level}'.encode())
io.recvuntil(b"signature: ")
io.sendline(b" ".join([str(r).encode(), str(s).encode()]))
c1 = io.recvline().decode()
print(c1)
level += 1



# =============Level 1=============
io.recvuntil(b"context: ")
io.sendline(b"")
msg = bytes.fromhex(io.recvline().split()[-1].decode())
r = eval(io.recvline().split()[-1].decode())
s = eval(io.recvline().split()[-1].decode())

# s = (pow(k, -1, n) * (z + r * priv)) % n
z = bytes_to_long(md5(msg).digest())
k1 = (E.lift_x(Integer(r))).log(G)
k2 = (-E.lift_x(Integer(r))).log(G)
priv = ((s*k1-z)*invert(r, n))%n
priv_i = ((s*k1-z)*invert(r, n))%n
if k1 != bytes_to_long(md5(str(priv).encode() + msg).digest()):
    priv = priv_i
r, s = Sign(priv, b'n1junior_2025', f'cat /flag{level}'.encode())
io.recvuntil(b"signature: ")
io.sendline(b" ".join([str(r).encode(), str(s).encode()]))
c1 = io.recvline().decode()
print(c1)
level += 1


# =============Level 2=============
t1 = 
t2 = 
tt1 = int(bytes_to_long(t1)*256**16%n)
tt2 = int(bytes_to_long(t2)*256**16%n)
io.recvuntil(b"context: ")
io.sendline(t1.hex().encode())
r1 = eval(io.recvline().split()[-1].decode())
s1 = eval(io.recvline().split()[-1].decode())

io.recvuntil(b"context: ")
io.sendline(t2.hex().encode())
r2 = eval(io.recvline().split()[-1].decode())
s2 = eval(io.recvline().split()[-1].decode())

# s = (pow(k, -1, n) * (z + r * priv)) % n
k1 = (E.lift_x(Integer(r1))).log(G)
k2 = (E.lift_x(Integer(r2))).log(G)
k11 = (-E.lift_x(Integer(r1))).log(G)
k22 = (-E.lift_x(Integer(r2))).log(G)
if abs(tt1-k1) > abs(tt1-k11):
    k1 = k11
if abs(tt2-k2) > abs(tt2-k22):
    k2 = k22
priv = ((s1*k1-s2*k2)*invert(r1-r2, n))%n
r, s = Sign(priv, b'n1junior_2025', f'cat /flag{level}'.encode())
io.recvuntil(b"signature: ")
io.sendline(b" ".join([str(r).encode(), str(s).encode()]))
c2 = io.recvline().decode()
print(c2)
level += 1


# =============Level 3=============
tt = []
t_int = [bytes_to_long(i) for i in tt]
io.recvuntil(b"context: ")
sh = []
R = PolynomialRing(GF(n), "k0, z, x0, y0, d")
k0, z, x0, y0, d = R.gens()
io.sendline(tt[0].hex().encode())
sh.append(eval(io.recvline().split()[-1].decode()))
eqs = [y0**2-(x0**3+3), sh[0]*k0-(z+x0*d)]
for i in range(1, 5):
    io.recvuntil(b"context: ")
    ki = k0 + (t_int[i]-t_int[0])*(256**16)
    del_k = (t_int[i]-t_int[0])*(256**16)*G
    del_kx, del_ky = del_k.xy()
    sl = (del_ky-y0)/(del_kx-x0)
    xi = sl**2-x0-del_kx
    io.sendline(tt[i].hex().encode())
    sh.append(eval(io.recvline().split()[-1].decode()))
    eqs.append((sh[i]*ki-(z+xi*d)).numerator())
# print("over")
I = R.ideal(eqs)
priv = I.groebner_basis()[-1]
# print(priv)
priv = int(-priv.coefficients()[-1])
r, s = Sign(priv, b'n1junior_2025', f'cat /flag{level}'.encode())
io.recvuntil(b"signature: ")
io.sendline(b" ".join([str(r).encode(), str(s).encode()]))
c3 = io.recvline().decode()
print(c3)

"""
flag0: 💧

flag1: 🐱

flag2: flag{**redacted**}

flag3: flag{**redacted1**}

"""

后续

因为是今天下午才开始写hhh，而且写得有点复杂，所以还没来得及看后面那两道，吃完饭再接着更新（确信）

image-20250915190050101

Thanks for reading!

N1junior2025-Crypto

Mon Sep 15 2025
2743 words · 20 minutes
CTF Crypto

© Shin | CC BY-NC-SA 4.0

Share this article

X (Twitter) Telegram Reddit Facebook Email

Table of Contents